Fine fitting functions

Source: R/doubleLogistics_R.R

double logistics, piecewise logistics and many other functions to curve fit VI time-series.

Logistic(par, t)

doubleLog.Zhang(par, t)

doubleLog.AG(par, t)

doubleLog.AG2(par, t)

doubleLog.Beck(par, t)

doubleLog.Elmore(par, t)

doubleLog.Gu(par, t)

doubleLog.Klos(par, t)

Arguments

par

A vector of parameters

t

A Date or numeric vector

Details

  • Logistic The traditional simplest logistic function. It can be only used in half growing season, i.e. vegetation green-up or senescence period.

  • doubleLog.Zhang Piecewise logistics, (Zhang Xiaoyang, RSE, 2003).

  • doubleAG Asymmetric Gaussian.

  • doubleLog.Beck Beck logistics.

  • doubleLog.Gu Gu logistics.

  • doubleLog.Elmore Elmore logistics.

  • doubleLog.Klos Klos logistics.

All of those function have par and formula attributes for the convenience for analytical D1 and D2

References

  1. Beck, P.S.A., Atzberger, C., Hogda, K.A., Johansen, B., Skidmore, A.K., 2006. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. https://doi.org/10.1016/j.rse.2005.10.021.

  2. Elmore, A.J., Guinn, S.M., Minsley, B.J., Richardson, A.D., 2012. Landscape controls on the timing of spring, autumn, and growing season length in mid-Atlantic forests. Glob. Chang. Biol. 18, 656-674. https://doi.org/10.1111/j.1365-2486.2011.02521.x.

  3. Gu, L., Post, W.M., Baldocchi, D.D., Black, TRUE.A., Suyker, A.E., Verma, S.B., Vesala, TRUE., Wofsy, S.C., 2009. Characterizing the Seasonal Dynamics of Plant Community Photosynthesis Across a Range of Vegetation Types, in: Noormets, A. (Ed.), Phenology of Ecosystem Processes: Applications in Global Change Research. Springer New York, New York, NY, pp. 35-58. https://doi.org/10.1007/978-1-4419-0026-5_2.

  4. Peter M. Atkinson, et al., 2012, RSE, 123:400-417

  5. https://github.com/cran/phenopix/blob/master/R/FitDoubleLogGu.R

Examples

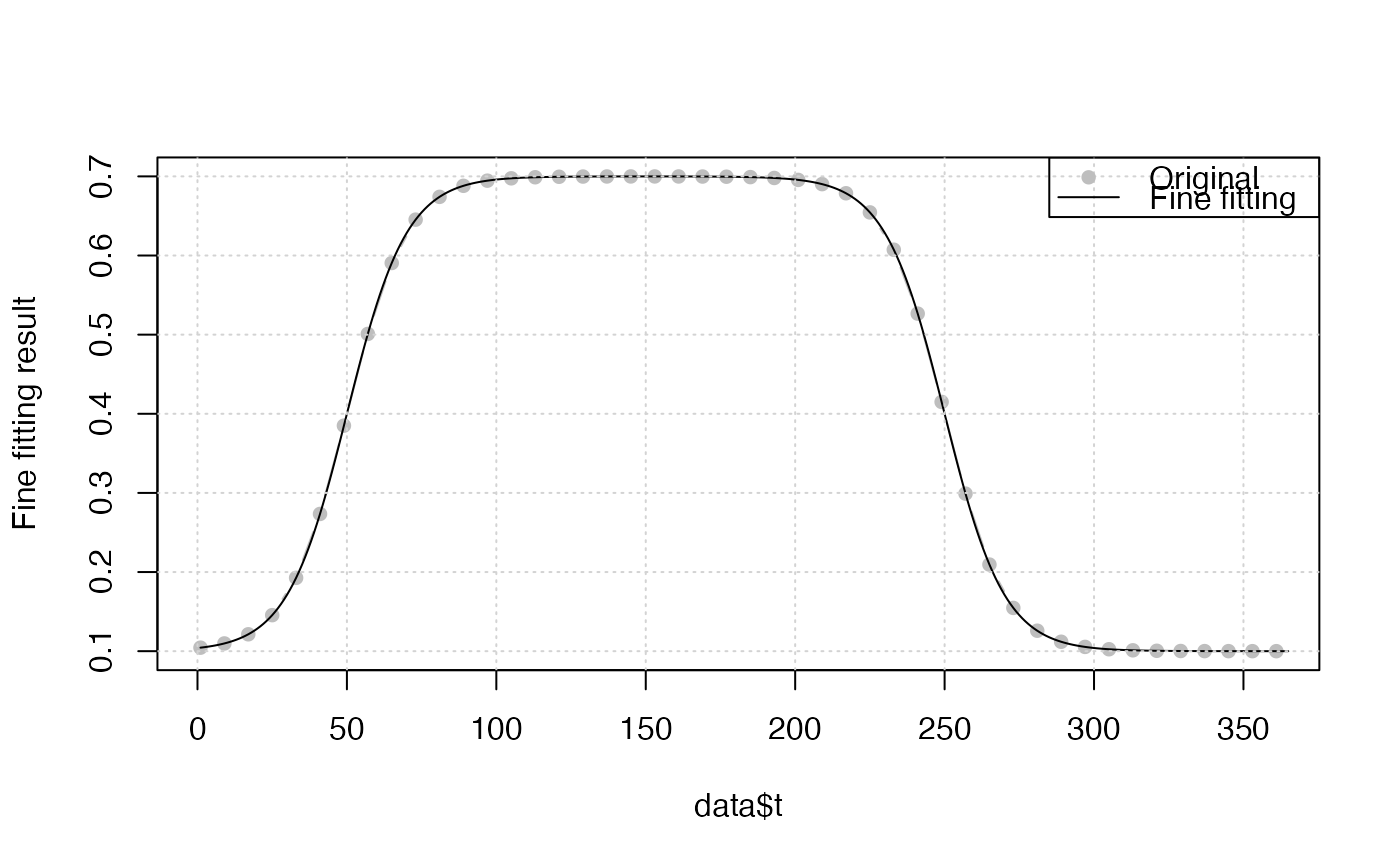
# simulate vegetation time-series
t    <- seq(1, 365, 8)
par  <- c(mn = 0.1, mx = 0.7, sos = 50, rsp = 0.1, eos = 250, rau = 0.1)
y    <- doubleLog.Beck(par, t)
data <- data.frame(t, y)
# methods <- c("AG", "Beck", "Elmore", "Gu", "Zhang")
tout <- seq(1, 365, 1)
r <- FitDL.Elmore(y, t, tout)

plot(r, data)

get_GOF(r, data)
#>       R2   NSE     R         RMSE pvalue n_sim
#>    <num> <num> <num>        <num>  <num> <num>
#> 1:     1     1     1 2.503802e-10      0    46
get_param(r)
#> # A tibble: 1 × 7
#>      mn    mx   sos   rsp   eos   rau    m7
#>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0.100 0.600  50.0 0.100  250. 0.100     0